Chapter 1
Units and Vectors: Tools for Physics
1.1 The Important Stuff
1.1 .1 The SI System
Physics is based on measurement. Measurements are made by comparisons to well–defined
standards which de fine the units for our measurements.
The SI system (popularly known as the metric s ystem) is the one used in physics. Its
unit of length is the meter, its unit of time is the second and its unit of mass is t he kilogram.
Other quantities in physics are derived from these. For exampl e the unit of energy is the
joule, defined by 1 J = 1
kg·m
2
s
2
.
As a convenience in using the SI system we can associate prefixes with the basic units to
represent powers of 10. The most commonly used prefixes are given here:
Factor Prefix Symbol
10
−12
pico- p
10
−9
nano- n
10
−6
micro- µ
10
−3
milli- m
10
−2
centi- c
10
3
kilo- k
10
6
mega- M
10
9
giga- G
Other basic units commonly used in physic s are:
Time : 1 minute = 60 s 1 hour = 60 min etc.
Mass : 1 atomic mass unit = 1 u = 1.6605 ×10
−27
kg
1

2 CHAPTER 1. UNITS AN D VECTORS: TOOLS FOR PHYSICS
1.1 .2 Changing Units
In all of our mathem atical operations we must always write down the units and we always
treat the unit symbols as multiplicative factors. For example, if me multiply 3.0 kg by 2.0
m
s
we get
(3.0 kg) · (2.0
m
s
) = 6.0
kg·m
s
We use the same idea in changing the units in which some physical quantity is expressed.
We can multiply the original quantity by a conversion factor, i.e. a ratio of values for
which the numerator is the same thing as the denominator. The conversion factor is then
equal to 1 , and so we do not change the original quantity when we multiply by the conversion
factor.
Examples of conversion factors are:
1 min
60 s
100 cm
1 m
1 yr
365.25 day
!
1 m
3.28 ft
1.1 .3 Density
A quantity which will be encountered in your study of liquids and solids is the density of a
sample. It is usually denoted by ρ and is defined as the ratio of mass to volume:
ρ =
m
V
(1.1)
The SI units of density are
kg
m
3
but you often see it expressed in
g
cm
3
.
1.1 .4 Dime nsional Analysis
Every equation that we use in physics must have the same type of units on both sides of the
equals sign. Our basic unit types (di mensions) are length (L), time (T ) and mass (M).
When we do dimensional analysis we focus on the units of a physics equation without
worrying about the numeric al values.
1.1 .5 Vectors; Vector Additio n
Many of the quantities we encounter in physics have both magnitude (“how much”) and
direction. These are vector quantities.
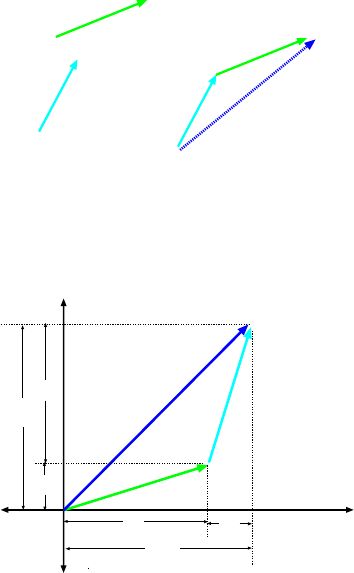
We can represent vectors graphicall y as arrows and then the sum of two vect ors is found
(graphically) by joining the head of one to the tail of the other and then connecting head to
tail for the combination, as shown in Fig. 1.1 . The sum of two (or more) vectors is often
called the result ant.
We can add vectors in any order we want: A + B = B + A. We say that vector addition
is “commutative”.
We express vectors in component form using the unit vectors i, j and k, which each
have magnitude 1 and point along the x, y and z axes of the coordinate system, respectively.
1.1. THE IMPORTANT STUFF 3
A
B
A
B
A+B
(a)
(b)
Figure 1.1: Vector addition. (a) shows the vectors A and B to be summed. (b) shows how to perform the
sum graphically.
B
C
A
A
x
B
y
A
y
B
x
C
y
C
x
x
y
Figure 1.2: Addition of vectors by components (in two dimensions).
Any vector can be expressed as a sum of multi ples of these basic vectors; for example,
for the vector A we would write:
A = A
x
i + A
y
j + A
z
k .
Here we would say that A
x
is the x component of the vector A; likewise for y and z.
In Fig. 1.2 we illustrate how we get the components for a vector which is the sum of two
other vectors. If
A = A
x
i + A
y
j + A
z
k and B = B
x
i + B
y
j + B
z
k
then
A + B = (A
x
+ B
x
)i + (A
y
+ B
y
)j + (A
z
+ B
z
)k (1.2)
Once we have found the (Cartesian) component of two vectors, additi on is si mple; just add
the corresponding components of the two vectors to get the components of the resultant
vector.
When we multiply a vector by a scalar, the scalar multiplies each component; If A is a
vector and n is a scalar, then
cA = cA
x
i + cA
y
j + cA
z
k (1.3)
4 CHAPTER 1. UNITS AN D VECTORS: TOOLS FOR PHYSICS
In terms of its components, the magnitude ( “l ength”) of a vector A (which we write as
A) is given by:
A =
q
A
2
x
+ A
2
y
+ A
2
z
(1.4)
Many of our physics problems will be in two dimensions (x and y) and then we can also
represent it in polar form. If A is a two–dimensional vector and θ as the angle that A
makes with t he +x axis measured counter-clockwise then we can express this vector in terms
of components A
x
and A
y
or in terms of its magnitude A and the angle θ. These descriptions
are related by:
A
x
= A cos θ A
y
= A sin θ (1.5)
A =
q
A
2
x
+ A
2
y
tan θ =
A
y
A
x
(1.6)
When we use Eq . 1.6 to find θ from A
x
and A
y
we need to be careful because the inverse
tangent operation (as done on a calcul ator) might give an angle in the wrong quadrant; one
must think about the signs of A
x
and A
y
.
1.1 .6 Multiplying Vectors
There are two ways to “multiply” two vectors together.
The scalar product (or dot product) of the vectors a and b is given by
a ·b = ab cos φ (1.7)
where a is the magnitude of a, b is the magnitude of b and φ is the angle between a and b.
The scalar product is commutative: a · b = b · a. One can show that a · b i s related to
the components of a and b by:
a · b = a
x
b
x
+ a
y
b
y
+ a
z
b
z
(1.8)
If two vectors are p erpendicular then their scalar product is zero.
The vector product (or cross product) of vectors a and b is a vector c whose mag-
nitude is given by
c = ab sin φ (1.9)
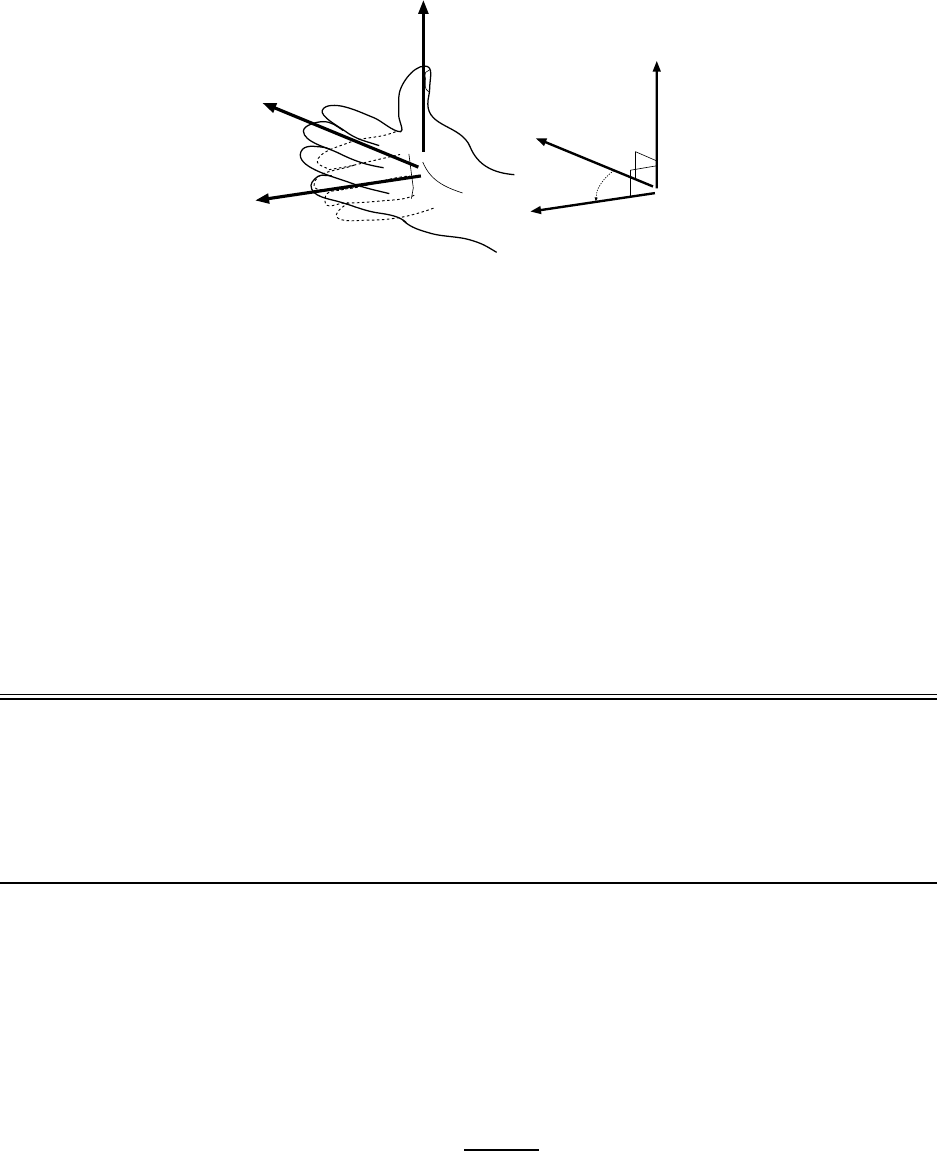
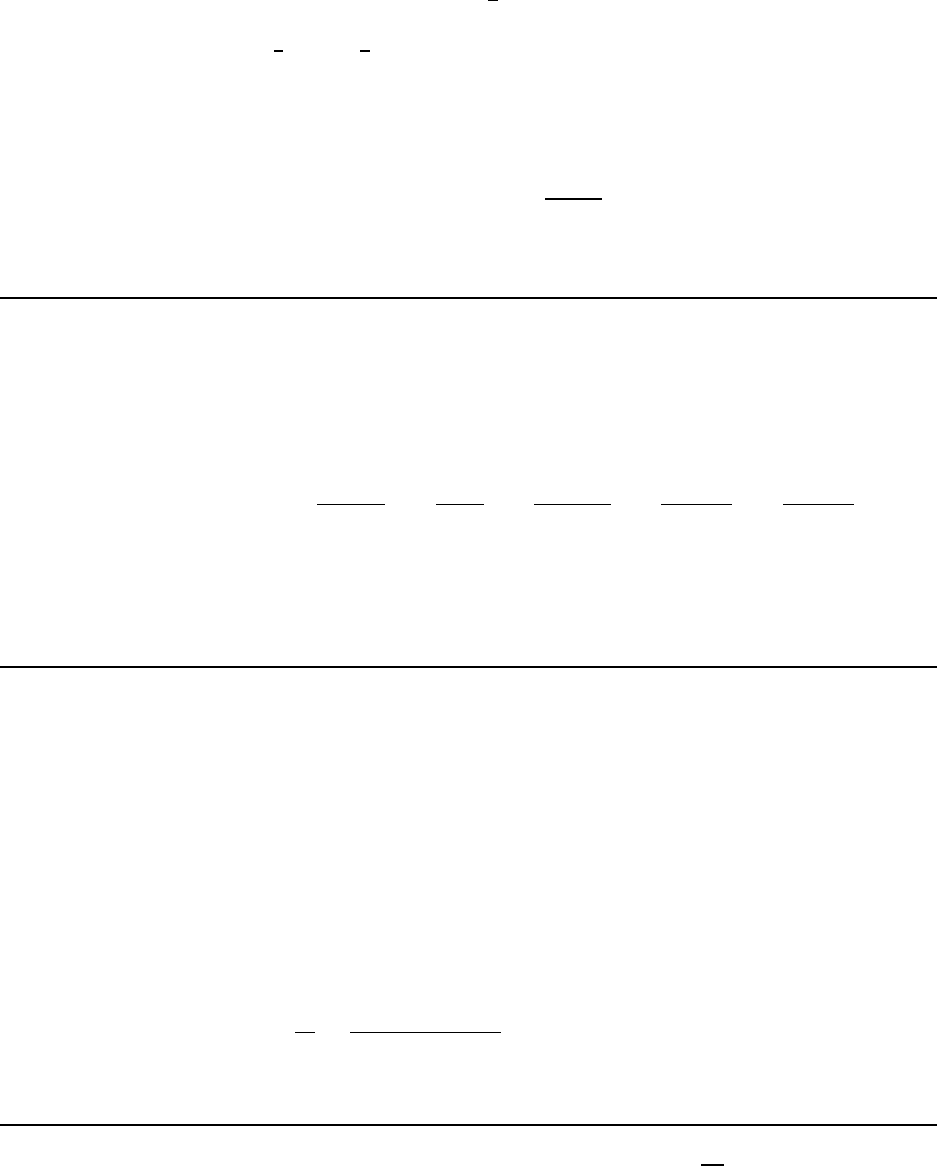
where φ is the s mallest angle between a and b. The direction of c is perpendicular to the
plane containing a and b with its orientation given by the right–hand rule. One way
of using the right–hand rule is to let the fingers of the right hand bend (in their natural
direct ion!) from a to b; the direction of the thumb is the dire ction of c = a × b. This is
illustrated in Fig. 1.3.
The vector product is anti–commutative: a × b = −b × a.
Relations among the unit vectors for vector products are:
i × j = k j × k = i k × i = j (1.10)
1.2. WORKED EXAM PLES 5
A
B
C
A
B
C
(a)
(b)
f
Figure 1.3: (a) Finding the directio n of A × B. Fingers of the right hand sweep from A to B in the
shortest and least painful way. The extended thumb points in the direction of C. (b) Vectors A, B and C.
The magnitude of C is C = AB sin φ.
The vector product of a and b can be computed from the components of these vectors
by:
a × b = (a
y
b
z
− a
z
b
y
)i + (a
z
b
x
− a
x
b
z
)j + (a
x
b
y
−a
y
b
x
)k (1.11)
which can be abbreviated by the notation of the de t erminant:
a × b =
i j k
a
x
a
y
a
z
b
x
b
y
b
z
(1.12)
1.2 Worked Ex amples
1.2 .1 Changing Units
1. The Empire State Building is 1472 ft high. Express this height in both meters
and centimeters. [FGT 1-4]
To do the first unit conversion (feet to meters), we can use the relation (see the Conversion
Factors in the back of this book):
1 m = 3.281 ft
We set up the conversion factor so that “ft” cancels and leaves meters:
1472 ft = (1472 ft)
1 m
3.281 ft
= 448.6 m .
So the height can be expressed as 448.6 m. To convert this to centimeters, use:
1 m = 100 cm

6 CHAPTER 1. UNITS AN D VECTORS: TOOLS FOR PHYSICS
and get:
448.6 m = (448.6 m)
100 cm
1 m
= 4.486 × 10
4
cm
The Empire State Building i s 4.486 × 10
4
cm high!
2. A rectangular building lot is 100.0 ft by 150.0 ft. Determine the area of this lot
in m
2
. [Ser4 1-19]
The area of a rectangle is j ust the product of its length and wi dth so the area of the lot
is
A = (100.0 ft)(150.0 ft) = 1.500 × 10
4
ft
2
To convert this to units of m
2
we can use the relation
1 m = 3.281 ft
but the conversion factor needs to be applied twice so as to c ancel “ ft
2
” and get “ m
2
”. We
write:
1.500 ×10
4
ft
2
= (1.500 × 10
4
ft
2
) ·
1 m
3.281 ft
2
= 1.393 × 10
3
m
2
The area of the lot is 1.393 × 10
3
m
2
.
3. The Earth is approximately a sphere of radius 6. 37 × 10
6
m. (a) What is its
circumference in kilometers? (b) What is i ts surface area in square kilometers?
(c) What is its volume i n cubic kilometers? [HRW5 1-6]
(a) The circumference of the sphere of radius R, i.e. the distance around any “great c ircle”
is C = 2πR. Using the given value of R we find:
C = 2πR = 2π(6.37 × 10
6
m) = 4.00 × 10
7
m .
To convert this to kilometers, use the relation 1 km = 10
3
m in a c onversion factor:
C = 4.00 × 10
7
m = (4.00 × 10
7
m) ·
1 km
10
3
m
!
= 4.00 × 10
4
km
The circumfer ence of the Earth is 4.00 × 10
4
km.
(b) The surface area of a sphere of radius R is A = 4πR
2
. So we get
A = 4πR
2
= 4π(6.37 × 10
6
m)
2
= 5.10 × 10
14
m
2
Again, use 1 km = 10
3
m but to cancel out t he uni ts “ m
2
” and replace them with “ km
2
” it
must be applied twice:
A = 5.10 × 10
14
m
2
= (5.10 × 10
14
m
2
) ·
1 km
10
3
m
!
2
= 5.10 × 10
8
km
2
1.2. WORKED EXAM PLES 7
The surface area of the Earth is 5.10 × 10
8
km
2
.
(c) The volume of a sphere of radius R is V =
4
3
πR
3
. So we get
V =
4
3
πR
3
=
4
3
π(6.37 × 10
6
m)
3
= 1.08 × 10
21
m
3
Again, use 1 km = 10
3
m but to cancel out the units “m
3
” and replace them wi t h “ km
3
” it
must be applied three tim es:
V = 1.08 × 10
21
m
3
= (1.08 × 10
21
m
3
) ·
1 km
10
3
m
!
3
= 1.08 × 10
12
km
3
The volume of the Earth is 1.08 × 10
12
km
3
.
4. Calculate the number of kilometers in 20.0 mi using only the following conver-
sion factors: 1 mi = 5280 ft, 1 ft = 12 in, 1 i n = 2.54 cm , 1 m = 100 cm, 1 km = 1000 m.
[HRW5 1- 7]
Set up the “factors of 1” as follows:
20.0 mi = (20.0 mi) ·
5280 ft
1 mi
!
·
12 in
1 ft
·
2.54 cm
1 in
·
1 m
100 cm
·
1 km
1000 m
!
= 32.2 km
Setting up the “factors of 1” in this way, all of the unit symbols cancel except for km
(kilometers) whi ch we keep as the units of the answer.
5. One gallon of paint (volume = 3.78 × 10
−3
m
3
) covers an area of 25.0 m
3
. What
is the thickness of the paint on the wall? [Ser4 1-31]
We will assume that the volume which the paint occupies while it’s covering the wall is
the sa me as it has when it is in t he can. (There are reasons why this may not be true, but
let’s just do this and proceed.)
The paint on the wall covers an area A and has a thickness τ; the volume occupi ed is t he
area time the thickness:
V = Aτ .
We have V and A; we just need to solve for τ :
τ =
V
A
=
3.78 × 10
−3
m
3
25.0 m
2
= 1.51 × 10
−4
m .
The thi ckness is 1.51 × 10
−4
m. This quantity can also be expressed as 0.151 mm.
6. A certain brand of house paint claims a coverage of 460
ft
2
gal
. (a) Express this
quantity in square meters per liter. (b) Express thi s quant ity in SI base units. (c)

8 CHAPTER 1. UNITS AN D VECTORS: TOOLS FOR PHYSICS
What i s the inverse of the original quantity, and what is its physical significance?
[HRW5 1- 15]
(a) U se the following relations in forming the c onversion factors: 1 m = 3.28 ft and 1000 liter =
264 gal. To get prope r cancellation of the units we set it up as:
460
ft
2
gal
= (460
ft
2
gal
) ·
1 m
3.28 ft
2
·
264 gal
1000 L
!
= 11.3
m
2
L
(b) Even though the units of the answer to part (a) are based on the m etric system, they
are not made from the base units of the SI system, which are m, s, and kg. To make the
complete conversion to SI units we need to use the re lation 1 m
3
= 1000 L. Then we get:
11.3
m
2
L
= (11.3
m
2
L
) ·
1000 L
1 m
3
= 1.13 × 10
4
m
−1
So the coverage can also be expressed (not so meaningfully, perhaps) as 1.13 × 10
4
m
−1
.
(c) The inverse (reciprocal ) of the q uantity as it was originally expressed is
460
ft
2
gal
−1
= 2.17 × 10
−3
gal
ft
2
.
Of course when we take t he reciprocal the units in the numerator and de nominator also
switch places!
Now, the first expression of the quantity tells us that 460 ft
2
are associated with every
gallon, that is, each gallon will provide 460 ft
2
of coverage. The new expression tells us that
2.17×10
−3
gal are associated with every ft
2
, that is, to cover one square foot of surface with
paint, one ne eds 2.17 × 10
−3
gallons of it.
7. Express the speed of light, 3.0 × 10
8
m
s
in (a) feet per nanosecond and (b)
millimeters per picosecond. [HRW5 1-19]
(a) For this conversion we can use the following facts:
1 m = 3.28 ft and 1 ns = 10
−9
s
to get:
3.0 ×10
8
m
s
= (3.0 × 10
8
m
s
) ·
3.28 ft
1 m
!
·
10
−9
s
1 ns
!
= 0.98
ft
ns
In these new units, the speed of l ight is 0.98
ft
ns
.
(b) For thi s conversion we can use:
1 mm = 10
−3
m and 1 ps = 10
−12
s
1.2. WORKED EXAM PLES 9
and set up the factors as follows:
3.0 × 10
8
m
s
= (3.0 × 10
8
m
s
) ·
1 mm
10
−3
m
·
10
−12
s
1 ps
!
= 3.0 × 10
−1
mm
ps
In these new units, the speed of l ight is 3.0 × 10
−1
mm
ps
.
8. One molecule of water (H
2
O) contains two atoms of hydrogen and one atom
of oxygen. A hydrogen atom has a mass of 1. 0 u and an atom of oxygen has a
mass of 16 u, approximately. (a) W hat is the mass in kilograms of one molecule
of water? (b) How many molecul es of water are in the world’s oceans, which
have an estimated total mass of 1.4 × 10
21
kg? [HRW5 1-33]
(a) We are given the masses of the atoms of H and O in atomic mass units; using these
values, one molecule of H
2
O has a mass of
m
H
2
O
= 2(1.0 u) + 16 u = 18 u
Use the relation between u (atomic mass units) and kilograms to convert this to kg:
m
H
2
O
= (18 u)
1.6605 × 10
−27
kg
1 u
!
= 3.0 × 10
−26
kg
One water molecule has a mass of 3.0 × 10
−26
kg.
(b) To get the number of molecules i n all the oceans, divide the mass of all the oceans’
water by the mass of one molecule:
N =
1.4 ×10
21
kg
3.0 × 10
−26
kg
= 4.7 × 10
46
.
. . . a large number of molec ules!
1.2 .2 Density
9. Calculate the density of a solid cube that measures 5.00 cm on each side and
has a mass of 350 g. [Ser4 1-1 ]
The volume of this cube is
V = ( 5.00 cm) · (5.00 cm) ·(5.00 cm) = 125 cm
3
So from Eq. 1.1 the density of the cube is
ρ =
m
V
=
350 g
125 cm
3
= 2.80
g
cm
3
10 CHAPTER 1. UNITS AN D VECTORS: TOOLS FOR PHYSICS
r
2
r
1
Figure 1.4: Cross–section of copper shell in Example 11.
10. The mass of the planet Saturn is 5.64 × 10
26
kg and its radius is 6.00 × 10
7
m.
Calculate its density. [S er4 1-2]
The planet Saturn is roughly a sphere. (But only roughly! Ac tually its shape is rather
distorted.) Using the formula for the volume of a sphere, we find the volume of Saturn:
V =
4
3
πR
3
=
4
3
π(6.00 × 10
7
m)
3
= 9.05 × 10
23
m
3
Now using the definit ion of density we find:
ρ =
m
V
=
5.64 × 10
26
kg
9.05 × 10
23
m
3
= 6.23 × 10
2
kg
m
3
While this answer is correct, it is useful to express the result i n units of
g
cm
3
. Using our
conversion factors in the usual way, we get:
6.23 × 10
2
kg
m
3
= (6.23 × 10
2
kg
m
3
) ·
10
3
g
1 kg
!
·
1 m
100 cm
3
= 0.623
g
cm
3
The average density of Saturn is 0.623
g
cm
3
. Interestingly, this is less than the density of
water.
11. How many grams of copper are required to make a hollow spherical shell
with an inner radius of 5.70 cm and an outer radius of 5.75 cm? The density of
copper is 8.93 g/ cm
3
. [Ser4 1-3]
A cross–section of the copper sphere is shown in Fig. 1.4. The outer and i nner radii are
noted as r
2
and r
1
, re spectively. We must find the volum e of space occupied by the copper
metal; thi s volume is the difference in the volumes of the two spherical surfaces:
V
cop per
= V
2
− V
1
=
4
3
πr
3
2
−
4
3
πr
3
1
=
4
3
π(r
3
2
− r
3
1
)
With the given values of the radii, we find:
V
cop per
=
4
3
π((5.75 cm)
3
− (5.70 cm)
3
) = 20.6 cm
3

1.2. WORKED EXAMPLES 11
Now use the definition of density to find the mass of t he copper contained i n the shell:
ρ =
m
cop per
V
cop per
=⇒ m
cop per
= ρV
cop per
=
8.93
g
cm
3
(20.6 cm
3
) = 184 g
184 grams of copper are required to make the spherical shell of the given dimensions.
12. One cubic meter ( 1. 00 m
3
) of aluminum has a mass of 2.70 ×10
3
kg, and 1.00 m
3
of iron has a mass of 7.86 × 10
3
kg. Find the radius of a solid aluminum sphere
that will balance a solid iron sphere of radius 2.00 cm on an equal–arm balance.
[Ser4 1-39]
In the statement of the problem, we are given the densities of aluminum and iron:
ρ
Al
= 2.70 × 10
3 kg
m
3
and ρ
Fe
= 7.86 × 10
3 kg
m
3
.
A solid iron sphere of radius R = 2.00 cm = 2.00 × 10
−2
m has a volume
V
Fe
=
4
3
πR
3
=
4
3
π(2.00 × 10
−2
m)
3
= 3.35 × 10
−5
m
3
so t hat from M
Fe
= ρ
Fe
V
Fe
we find the mass of the iron sphere:
M
Fe
= ρ
Fe
V
Fe
=
7.86 × 10
3
kg
m
3
(3.35 × 10
−5
m
3
) = 2.63 ×10
−1
kg
If this sphere balances one made from aluminum in an “equal–arm balance”, then they
have the same mass. So M
Al
= 2.63 × 10
−1
kg is the mass of the aluminum sphere. From
M
Al
= ρ
Al
V
Al
we can find its volume:
V
Al
=
M
Al
ρ
Al
=
2.63 × 10
−1
kg
2.70 × 10
3
kg
m
3
= 9.76 × 10
−5
m
3
Having the volume of the sphere, we can find its radius:
V
Al
=
4
3
πR
3
=⇒ R =
3V
Al
4π
1
3
This gives:
R =
3(9.76 × 10
−5
m
3
)
4π
!
1
3
= 2.86 × 10
−2
m = 2.86 cm
The aluminum sphere must have a radius of 2.86 cm to balance the iron sphere.

12 CHAPTER 1. UNITS AN D VECTORS: TOOLS FOR PHYSICS
1.2 .3 Dime nsional Analysis
13. The period T of a simple pendulum is measured in tim e units and is
T = 2π
s
`
g
.
where ` is the length of the pendulum and g is the free–fal l acceleration in units
of length divide d by t he square of time. Show that this equation is dimensionally
correct. [Ser4 1- 14]
The period (T ) of a pendulum is the amount of time i t takes to makes one full swing
back and forth. It i s measured in units of time so its dimensions are represented by T .
On the right side of the equation we have the length `, whose dimensions are represented
by L. We are told that g is a length divi ded by the square of a time so its dimensions must
be L/T
2
. There is a factor of 2π on the right side, but this is a pure number and has no
units. So the dimensions of the right side are:
v
u
u
t
L
L
T
2
=
√
T
2
= T
so that the right hand side must also have units of time. Both sides of the equation agree in
their units, which must b e true for it to be a valid equation!
14. The volume of an object as a function of time is calculated by V = At
3
+ B/t,
where t is time measured in seconds and V is in cubic meters. Determine the
dimension of the constants A and B. [Ser4 1-15]
Both sides of the equation for volume must have the same dimensions, and those must
be the dimensions of volume where are L
3
(SI units of m
3
). Since we can only add terms
with the same dimensions, each of the terms on right side of the equation (At
3
and B/t)
must have t he same dimensions, namely L
3
.
Suppose we denote the units of A by [A]. Then our comment about the dimensions of
the first term gives us:
[A]T
3
= L
3
=⇒ [A] =
L
3
T
3
so A has dimensions L
3
/T
3
. In the SI system, it would have units of m
3
/ s
3
.
Suppose we denote the unit s of B by [B]. Then our comment about the dime nsions of
the second term gives us:
[B]
T
= L
3
=⇒ [B] = L
3
T
so B has dimensions L
3
T . In the SI sy stem, it would have units of m
3
s.

1.2. WORKED EXAMPLES 13
15. Newton’s law of universal gravitation is
F = G
Mm
r
2
Here F is the force of gravity, M and m are masses, and r is a length. Force has
the SI units of kg · m/s
2
. What are the SI units of the constant G? [ Ser4 1-17]
If we denote the dimensions of F by [ F ] (and the same for the other quantities) then
then dimensions of the quantities in Newton’s Law are:
[M] = M ( mass) [m] = M [r] = L [F ] :
ML
T
2
What we don’t know (yet) is [G], the dimensions of G. Putti ng the known di mensions into
Newton’s Law, we must have:
ML
T
2
= [G]
M · M
L
2
since the dimensions must be the same on both sides. Doing some algebra with the dimen-
sions, this gives:
[G] =
ML
T
2
L
2
M
2
=
L
3
MT
2
so t he dimensions of G are L
3
/(MT
2
). In the SI system, G has units of
m
3
kg · s
3
16. In quantum m echanics, the fundamental constant called Planck’s constant,
h, has dimensions of [ML
2
T
−1
]. Construct a quantity wit h the dimensions of
length from h, a mass m , and c, the speed of light . [FGT 1-54]
The problem suggests that there is some product of powers of h, m and c which has
dimensions of length. If these powers are r, s and t , respectively, then we are looking for
values of r, s and t such that
h
r
m
s
c
t
has dimensions of length.
What are the dimensions of this product, as written? We were given the dimensions of
h, namely [ ML
2
T
−1
]; the dimensions of m are M, and the dimensions of c are
L
T
= LT
−1
(it
is a speed). So the dimensions of h
r
m
s
c
t
are:
[ML
2
T
−1
]
r
[M]
s
[LT
−1
]
t
= M
r+s
L
2r+t
T
−r−t
where we have used the laws of combining exponents which we all remember from algebra.

14 CHAPTER 1. UNITS AN D VECTORS: TOOLS FOR PHYSICS
Now, since this is supposed to have dimensions of length, the power of L must be 1 but
the other powers are zero. This gives the equations:
r + s = 0
2r + t = 1
−r − t = 0
which is a set of three equations for thre e unk nowns. Easy to solve!
The last of them gives r = −t. Substituting this into the sec ond equation gives
2r + t = 2(−t) + t = −t = 1 =⇒ t = −1
Then r = +1 and the first equation gi ves us s = −1. With these values, we can confidently
say that
h
r
m
s
c
t
= h
1
m
−1
c
−1
=
h
mc
has units of length.
1.2 .4 Vectors; Vector Additio n
17. (a) What is the sum in unit–vector notation of the two vectors a = 4.0i + 3.0j
and b = −13.0i + 7.0j? (b) What are the magnitude and direction of a + b? [HRW5
3-20]
(a) Summing the corresponding components of vectors a and b we find:
a + b = (4.0 − 13.0)i + (3.0 + 7.0)j
= −9.0i + 10.0j
This is the sum of the two vectors is unit–vector form.
(b) Using our results from (a), the magnitude of a + b is
|a + b| =
q
(−9.0)
2
+ (10.0)
2
= 13.4
and if c = a + b points in a direction θ as measured from the positive x axis, then the
tangent of θ is found from
tan θ =
c
y
c
x
= −1.11
If we naively take the arctangent using a calculator, we are told:
θ = tan
−1
(−1.11) = −48.0
◦
which is not correct because (as shown in Fig. 1.5), with c
x
negative, and c
y
positive, the
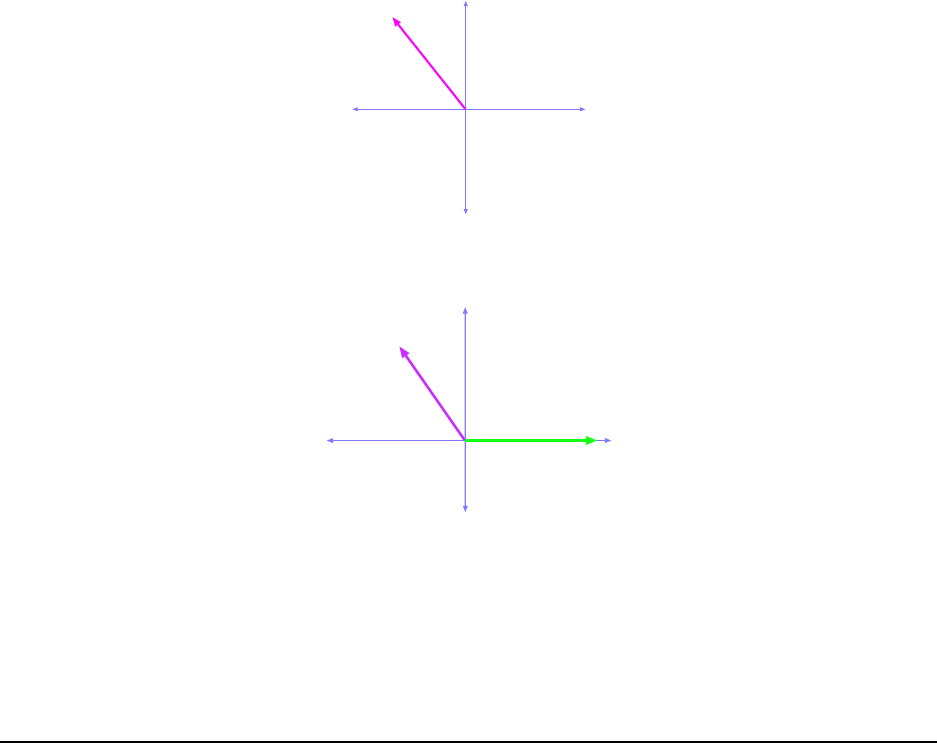
1.2. WORKED EXAMPLES 15
c
x
y
Figure 1.5: Vector c, found in Example 1 7. W ith c
x
= −9.0 and c
y
= +10.0, the direction of c is in the
second quadrant.
x
y
b
a
4.0 m
5.0 m
N
E
W
S
35
o
Figure 1.6: Vectors a and b as given in Example 1 8.
correct angle must be i n the s eco nd quadrant. The calculator was fooled because angles
which differ by multiples of 180
◦
have the same tangent. The direction we really want is
θ = −48.0
◦
+ 180.0
◦
= 132.0
◦
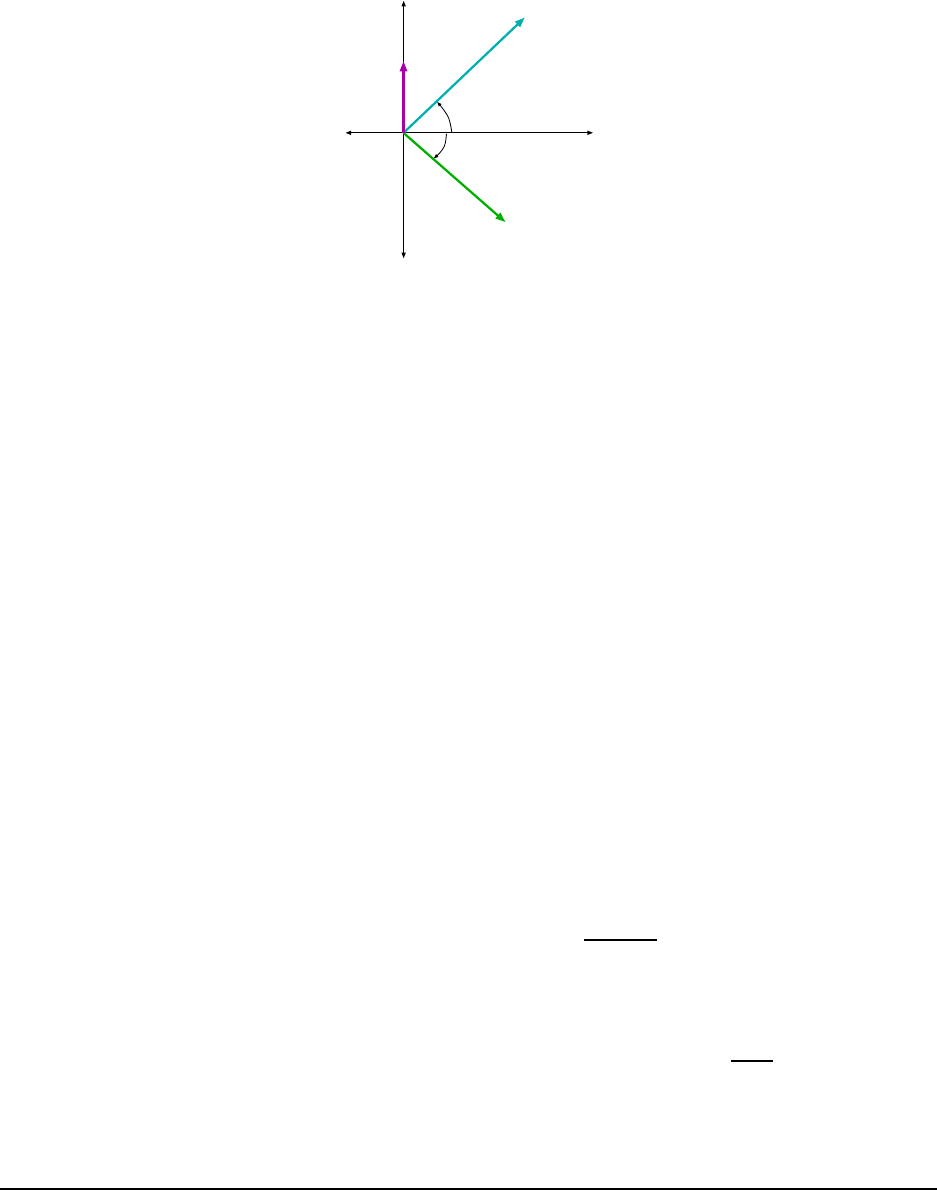
18. Vector a has magnitude 5.0 m and is directed east. Vector b has magnitude
4.0 m and is directed 35
◦
west of north. What are (a) the magnitude and (b) the
direction of a + b? What are (c) the magnit ude and (d) the direction of b − a?
Draw a vector diagram for each combination. [HRW6 3- 15]
(a) The vectors are shown in Fig. 1.6. (On the axes are shown the common direct ions N, S,
E, W and also the x and y axe s; “North” is the positive y direction, “East” is the positive
x direction, etc.) Expressing the vectors in i, j notation, we have:
a = (5.00 m)i
and
b = −( 4.00 m) sin 35
◦
+ (4.00 m) c os 35
c
irc
= (−2.29 m)i + (3.28 m)j
So if vector c is the sum of vectors a and b then:
c
x
= a
x
+ b
x
= (5.00 m) + (−2. 29 m) = 2.71 m
c
y
= a
y
+ b
y
= (0.00 m) + (3.28 m) = 3.28 m

16 CHAPTER 1. UNITS AN D VECTORS: TOOLS FOR PHYSICS
x
y
b
a
N
E
W
S
x
y
b
-a
N
E
W
S
(a)
(b)
c
d
Figure 1.7: (a) Vector diagram showing the addition a + b. (b) Vector diagram showing b − a.
The magnitude of c is
c =
q
c
2
x
+ c
2
y
=
q
(2.71 m)
2
+ (3.28 m)
2
= 4.25 m
(b) If the direction of c, as measured counterclockwise from the +x axis is θ the n
tan θ =
c
y
c
x
=
3.28 m
2.71 m
= 1.211
then the tan
−1
operation on a calculator gives
θ = tan
−1
(1.211) = 50.4
◦
and since vector c must lie in the first quadrant this angle i s correct. We note that this angle
is
90.0
◦
−50.4
◦
= 39.6
◦
just shy of the +y axis (the “North” dire ction). So we can also express the direction by
saying it is “39.6
◦
East of North”.
A vector diagram showing a, b and c is given in Fig. 1.7(a).
(c) If the vector d is given by d = b − a then the components of d are given by
d
x
= b
x
−a
x
= (−2.29 m) − (5. 00 m) = −7.29 m
c
y
= a
y
+ b
y
= (3.28 m) − (0.00 m) + (3.28 m) = 3.28 m
The magnitude of c is
d =
q
d
2
x
+ d
2
y
=
q
(−7.29 m)
2
+ (3.28 m)
2
= 8.00 m
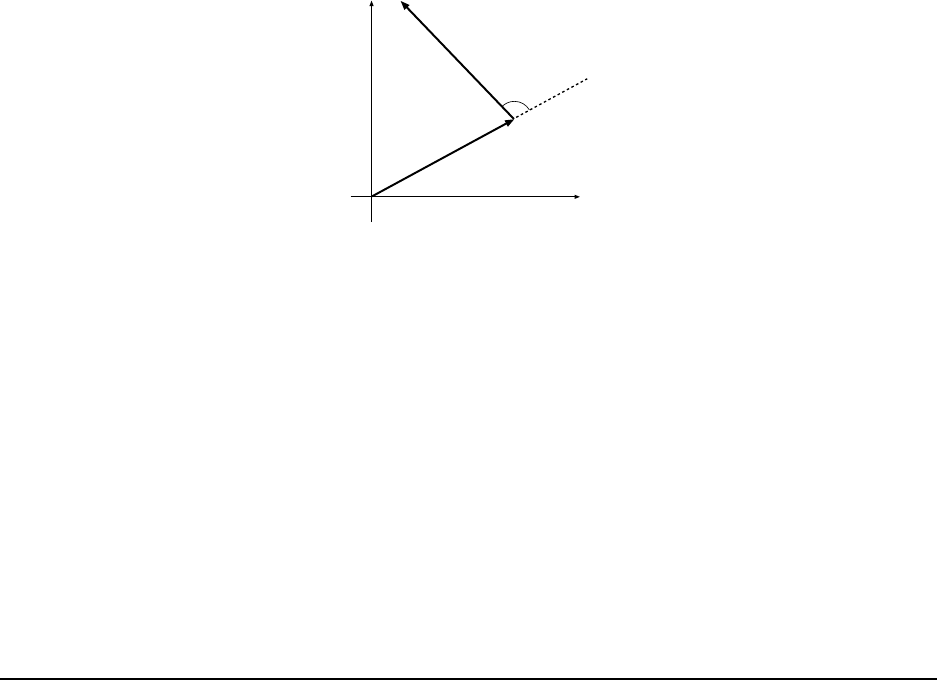
(d) If the direction of d, as measured counterclockwise from the +x axi s is θ then
tan θ =
d
y
d
x
=
3.28 m
−7.29 m
= −0.450
1.2. WORKED EXAMPLES 17
y
x
30
o
105
o
a
b
Figure 1.8: Vectors for Example 19.
Naively pushing buttons on the calculator gives
θ = tan
−1
(−0.450) = −24.2
◦
which can’t be right because from the signs of its components we know that d must lie in the
second quadrant. We need to add 180
◦
to get the correct answer for the t an
−1
operation:
θ = −24.2
◦
+ 180.0
◦
= 156
◦
But we note that this angle i s
180
◦
−156
◦
= 24
◦
shy of the −y axis, so the dire ction can also be ex pressed as “24
◦
North of West”.
A vector diagram showing a, b and d is given i n Fig. 1.7(b).
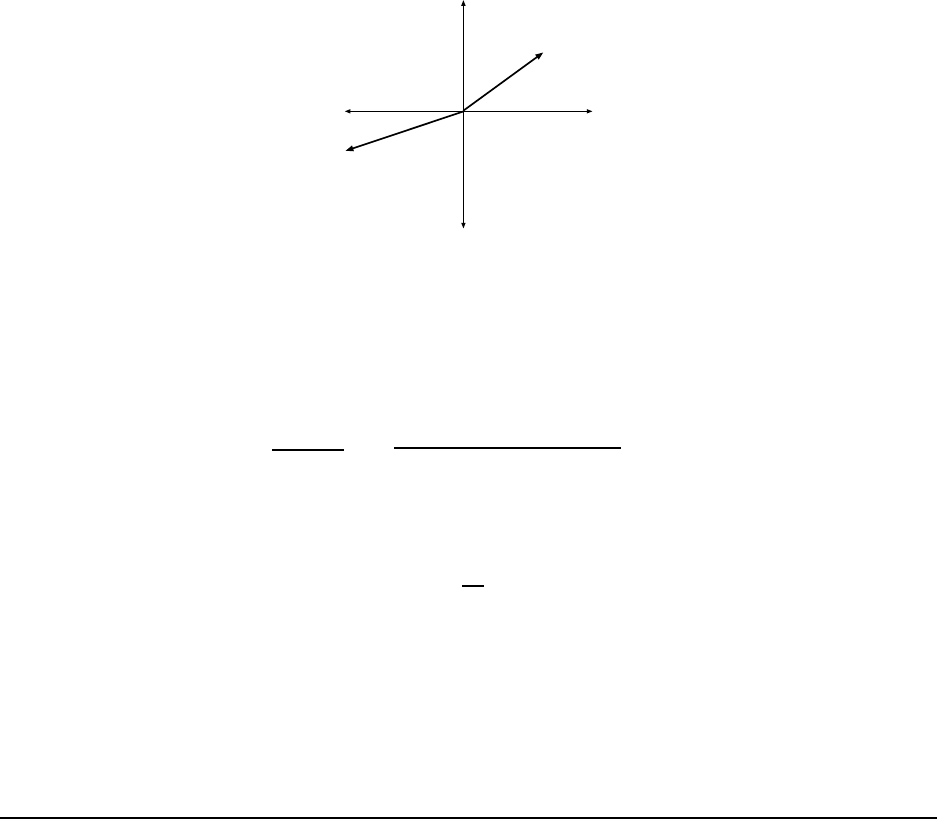
19. The two vectors a and b in Fi g. 1.8 have equal magnitude s of 10.0 m. Find
(a) the x component and ( b) the y component of their vector sum r, (c) the
magnitude of r and (d) the angle r m akes with the posi tive direction of the x
axis. [HRW6 3-21]
(a) First, find the x and y components of t he vectors a and b. The vector a makes an angle
of 30
◦
with the +x axis, so its components are
a
x
= a cos 30
◦
= (10.0 m) cos 30
◦
= 8.66 m
a
y
= a sin 30
◦
= (10.0 m ) sin 30
◦
= 5.00 m
The vector b makes an angle of 135
◦
with the +x axis ( 30
◦
plus 105
◦
more) so its components
are
b
x
= b cos 135
◦
= (10.0 m ) cos 135
◦
= −7.07 m
b
y
= b sin 135
◦
= (10.0 m ) sin 135
◦
= 7.07 m
Then if r = a + b, the x and y components of the vector r are:
r
x
= a
x
+ b
x
= 8.66 m − 7.07 m = 1.59 m
r
y
= a
y
+ b
y
= 5.00 m + 7.07 m = 12.07 m
18 CHAPTER 1. UNITS AN D VECTORS: TOOLS FOR PHYSICS
A
12.0 m
C
15.0 m
40.0
o
20.0
o
y
x
Figure 1.9: Vectors A and C as described in Example 2 0.
So the x component of the sum is r
x
= 1.59 m, and. . .
(b) . . . the y component of t he sum is r
y
= 12.07 m.
(c) The magnitude of the vector r is
r =
q
r
2
x
+ r
2
y
=
q
(1.59 m)
2
+ (12.07 m)
2
= 12.18 m
(d) To get the direction of the vector r expressed as an angle θ measured from the +x axis,
we note:
tan θ =
r
y
r
x
= 7.59
and then take the inverse tangent of 7.59:
θ = tan
−1
(7.59) = 82.5
◦
Since the components of r are both positive, the vector does lie in the first quadrant so that
the inverse tangent ope r ation has (this time) given the correct answer. So the directi on of r
is given by θ = 82.5
◦
.
20. In the sum A + B = C, vector A has a magnitude of 12.0 m and is angled 40.0
◦
counterclockwise from the +x direction, and vector C has magnitude of 15.0 m
and is angled 20.0
◦
counterclockwise from the −x direction. What are (a) the
magnitude and (b) the angle (relati ve to +x) of B? [HRW6 3- 22]
(a) Vectors A and C are diagrammed in Fig. 1.9. From these we can get t he components
of A and C (watch the signs on vector C from the odd way that its angle is gi ven!):
A
x
= (12.0 m ) cos(40.0
◦
) = 9.19 m A
y
= (12.0 m ) sin(40.0
◦
) = 7.71 m
C
x
= −(15.0 m) cos(20.0
◦
) = −14.1 m C
y
= −(15.0 m) sin(20.0
◦
) = −5.13 m
(Note, the vectors in this problem have units to go along with their magnitudes, namely m
(mete r s).) Then from the r elation A + B = C it follows that B = C −A, and from this we
find the components of B:
B
x
= C
x
− A
x
= −14.1 m − 9.19 m = −23.3 m

1.2. WORKED EXAMPLES 19
B
y
= C
y
− A
y
= −5.13 m − 7.71 m = −12.8 m
Then we find the magnitude of vector B:
B =
q
B
2
x
+ B
2
y
=
q
(−23.3)
2
+ (−12.8)
2
m = 26.6 m
(b) We find the direc t ion of B from:
tan θ =
B
y
B
x
= 0.551
If we naively press the “atan” button on our cal culators to get θ, we are told:
θ = tan
−1
(0.551) = 28.9
◦
(?)
which cannot be correct because from the components of B (both negative) we know that
vector B lies in the third quadrant. So we nee d to ad 180
◦
to the naive result t o get the
correct answer:
θ = 28.9
◦
+ 180.0
◦
= 208.9
◦
.
This is the angle of B , measured counterclockwise from the +x axis.
21. If a − b = 2c, a + b = 4c and c = 3i + 4j, then what are a and b? [HRW5 3-2 4]
We notice that i f we add the first two relations together, the vector b will cancel:
(a − b) + (a + b) = (2c) + (4c)
which gives:
2a = 6c =⇒ a = 3c
and we can use the last of the given equations to substitute for c; we get
a = 3c = 3(3i + 4j) = 9i + 12j
Then we can re arrange the first of the equations to solve for b:
b = a − 2c = (9i + 12j) − 2(3i + 4j)
= (9 −6)i + (12 − 8)j
= 3i + 4j
So we have found:
a = 9i + 12j and b = 3i + 4j
22. If A = (6.0i − 8.0j) units, B = (−8.0i + 3.0j) units, and C = (26.0i + 19.0j) units,
deter mine a and b so that aA + bB + C = 0. [Ser4 3-46]
20 CHAPTER 1. UNITS AN D VECTORS: TOOLS FOR PHYSICS
A
B
C
y
x
45
0
45
0
Figure 1.10: Vectors for Example 23
The condition on the vectors gi ven in the problem:
aA + bB + C = 0
is a condition on the individual components of the vectors. I t i mplie s:
aA
x
+ bB
x
+ C
x
= 0 and aA
y
+ bB
y
+ C
y
= 0 .
So that we have the equations:
6.0a − 8.0b + 26.0 = 0
−8.0a + 3.0b + 19.0 = = 0
We have two equations for two unk nowns so we can find a and b. The are lots of ways
to do this; one could multiply the first equation by 4 and the second equation by 3 to get:
24.0a − 32.0b + 104.0 = 0
−24.0a + 9.0b + 57.0 = = 0
Adding these gives
−23.0b + 161 = 0 =⇒ b =
−161.0
−23.0
= 7.0
and then the first of the origi nal equations gives us a:
6.0a = 8.0b − 26.0 = 8.0(7.0) − 26.0 = 30.0 =⇒ a =
30.0
6.0
= 5.0
and our solution is
a = 7.0 b = 5.0
23. Three vectors are oriented as shown in Fig. 1.10, where |A| = 20.0 units,
|B| = 40.0 units, and |C| = 30.0 units. Find (a) t he x and y components of the

1.2. WORKED EXAMPLES 21
resultant vector and (b) the magnitude and direction of the resultant vector.
[Ser4 3-47]
(a) Let’s first put these vectors into “unit–vector notation”:
A = 20.0j
B = (40.0 cos 45
◦
)i + (40.0 sin 45
◦
)j = 28.3i + 28.3j
C = (30.0 cos(−45
◦
))i + (30.0 sin(−45
◦
))j = 21.2i − 21.2j
Adding the components together, the resultant (total) vector is:
Resultant = A + B + C
= (28.3 + 21.2)i + (20.0 + 28.3 − 21.2)j
= 49.5i + 27.1j
So the x component of the resultant vector is 49.5 and the y component of the result ant is
27.1.
(b) If we call the resultant vector R, the n the magnitude of R is given by
R =
q
R
2
x
+ R
2
y
=
q
(49.5)
2
+ (27.1)
2
= 56.4
To find its direction (given by θ, measured counterclockwise from the x axis), we find:
tan θ =
R
y
R
x
=
27.1
49.5
= 0.547
and then taking the inverse tangent gi ves a possible answer for θ:
θ = tan
−1
(0.547) = 28.7
◦
.
Is this the right answer for θ? Since both components of R are positive, it must lie in the
first quadrant and so θ must be between 0
◦
and 90
◦
. So the direction of R is given by 28.7
◦
.
24. A vector B, when added to the vector C = 3.0i + 4.0j, y ields a resultant vector
that is in the posit ive y direc tion and has a magnitude equal to that of C. What
is the magnitude of B? [HRW5 3-26]
If the vector B is denoted by B = B
x
i + B
y
j then the resultant of B and C is
B + C = (B
x
+ 3.0)i + (B
y
+ 4.0)j .
We are told that the resultant points in the positive y direction, so its x component must
be zero. Then:
B
x
+ 3.0 = 0 =⇒ B
x
= −3.0 .

22 CHAPTER 1. UNITS AN D VECTORS: TOOLS FOR PHYSICS
Now, the magnitude of C is
C =
q
C
2
x
+ C
2
y
=
q
(3.0)
2
+ (4.0)
2
= 5.0
so t hat if the magnitude of B + C is also 5.0 then we get
|B + C| =
q
(0)
2
+ (B
y
+ 4.0)
2
= 5.0 =⇒ (B
y
+ 4.0)
2
= 25.0 .
The last e quation gives (B
y
+ 4.0) = ±5.0 and apparently there are two possible answers
B
y
= +1.0 and B
y
= −9.0
but the second case gives a resultant vector B + C which points in the negative y direction
so we omit it. Then with B
y
= 1.0 we find the magnitude of B:
B =
q
(B
x
)
2
+ (B
y
)
2
=
q
(−3.0)
2
+ (1.0)
2
= 3.2
The magnitude of vector B is 3.2.
1.2 .5 Multiplying Vectors
25. Vector A e xtends from the origin to a point having polar coordinates (7, 70
◦
)
and vector B extends from the origin to a point having polar coordinates ( 4, 130
◦
).
Find A · B . [S er4 7-13]
We can use Eq. 1.7 to find A · B. We have the magnitudes of the two vectors (namely
A = 7 and B = 4) and the angle φ between the two is
φ = 130
◦
− 70
◦
= 60
◦
.
Then we get:
A ·B = AB cos φ = (7)(4) cos 60
◦
= 14
26. Find the angle between A = −5i − 3j + 2k and B = −2j − 2k. [Ser4 7-20]
Eq. 1.7 allows us to find the cosine of the angle between two vectors as long as we know
their magnitudes and their dot product. The magnitudes of the vectors A and B are:
A =
q
A
2
x
+ A
2
y
+ A
2
z
=
q
(−5)
2
+ (−3)
2
+ (2)
2
= 6.164
B =
q
B
2
x
+ B
2
y
+ B
2
z
=
q
(0)
2
+ (−2)
2
+ (−2)
2
= 2.828
and their dot product is:
A · B = A
x
B
x
+ A
y
B
y
+ A
z
B
z
= (−5)(0) + (−3)(−2) + ( 2)(−2) = 2

1.2. WORKED EXAMPLES 23
Then from Eq. 1.7, if φ is the angle b etween A and B, we have
cos φ =
A · B
AB
=
2
(6.164)(2.828)
= 0.114
which then gives
φ = 83.4
◦
.
27. Two vector s a and b have the components, in arbitrary units, a
x
= 3.2,
a
y
= 1.6, b
x
= 0.50, b
y
= 4.5. (a) Find t he angle between the directions of a and
b. (b) Find the compone nts of a vector c that is perpendicular to a, is in the xy
plane and has a magnitude of 5.0 units. [HRW5 3-51]
(a) The scalar product has something to do with the angle between two vectors... if the
angle between a and b is φ then from Eq. 1. 7 we have:
cos φ =
a · b
ab
.
We can compute the right–hand–side of this equation since we know the components of a
and b. First, find a · b. Using Eq. 1.8 we find:
a · b = a
x
b
x
+ a
y
b
y
= (3.2)(0.50) + (1.6)(4.5)
= 8.8
Now find the magnitudes of a and b:
a =
q
a
2
x
+ a
2
y
=
q
(3.2)
2
+ (1.6)
2
= 3.6
b =
q
b
2
x
+ b
2
y
=
q
(0.50)
2
+ (4.5)
2
= 4.5
This gives us:
cos φ =
a · b
ab
=
8.8
(3.6)(4.5)
= 0.54
From which we get φ by:
φ = cos
−1
(0.54) = 57
◦
(b) Let the components of the vector c be c
x
and c
y
(we are told that it lies in the xy plane).
If c is perpendicular to a then the dot product of the two vectors must give ze ro. This tells
us:
a · c = a
x
c
x
+ a
y
c
y
= (3.2)c
x
+ (1.6)c
y
= 0
This equation doesn’t allow us to solve for the components of c but it does give us:
c
x
= −
1.6
3.2
c
y
= −0.50c
y

24 CHAPTER 1. UNITS AN D VECTORS: TOOLS FOR PHYSICS
Since the vector c has magnitude 5.0, we know that
c =
q
c
2
x
+ c
2
y
= 5.0
Using the previous equation to substitute for c
x
gives:
c =
q
c
2
x
+ c
2
y
=
q
(−0.50 c
y
)
2
+ c
2
y
=
q
1.25 c
2
y
= 5.0
Squaring the last line gives
1.25c
2
y
= 25 =⇒ c
2
y
= 20. =⇒ c
y
= ±4.5
One must be careful... the r e are two possible solutions for c
y
here. If c
y
= 4.5 then we have
c
x
= −0.50 c
y
= (−0.50)(4.5) = −2.2
But if c
y
= −4.5 then we have
c
x
= −0.50 c
y
= (−0.50)(−4.5) = 2.2
So the two possibilities for the vector c are
c
x
= −2.2 c
y
= 4.5
and
c
x
= 2.2 c
y
= −4.5
28. Two vectors are given by A = −3i + 4j and B = 2i + 3j. Find (a) A × B and
(b) the angle between A and B. [Ser4 11-7]
(a) Se tt ing up the determinant in Eq. 1. 12 (or just using Eq. 1.11 for the cross product) we
find:
A ×B =
i j k
−3 4 0
2 3 0
= (0 − 0)i + (0 − 0)j + ((−9) − (8))k = −17k
(b) To get the angle between A and B it is easiest to use the dot product and Eq. 1.7. The
magnitudes of A and B are:
A =
q
A
2
x
+ A
2
y
=
q
(−3)
2
+ (4)
2
= 5 B =
q
B
2
x
+ B
2
y
=
q
(2)
2
+ (3)
2
= 3.61

1.2. WORKED EXAMPLES 25
and the dot product of the two vectors is
A · B = A
x
B
x
+ A
y
B
y
+ A
z
B
z
= (−3)(2) + (4)(3) = 6
so t hen if φ is the angle between A and B we get:
cos φ =
A · B
AB
=
6
(5)(3.61)
= 0.333
which gives
φ = 70.6
◦
.
29. Prove that two vect ors must have equal magnitudes if their sum is perpen-
dicular t o their difference. [HRW6 3-23]
Suppose the condition stated in this problem holds for the two vectors a and b. If the
sum a + b is perp endicular to the difference a −b then the dot product of these two vectors
is zero:
(a + b) · (a − b) = 0
Use the distributive property of the dot product to e xpand the left side of this equation. We
get:
a · a − a · b + b · a −b ·b
But the dot product of a vector with itsel f gives the magnitude squared:
a · a = a
2
x
+ a
2
y
+ a
2
z
= a
2
(likewise b · b = b
2
) and the dot produc t is commutative: a · b = b · a. Using these facts,
we then have
a
2
− a · b + a · b + b
2
= 0 ,
which gives:
a
2
− b
2
= 0 =⇒ a
2
= b
2
Since the magnitude of a vector must be a positive number, this implies a = b and so vectors
a and b have t he same magnitude.
30. For the following three vect ors, what is 3C · (2A × B) ?
A = 2.00i + 3.00j − 4.00k
B = −3.00i + 4.00j + 2.00k C = 7.00i − 8.00j
[HRW6 3- 36]

26 CHAPTER 1. UNITS AN D VECTORS: TOOLS FOR PHYSICS
Actually, from the properties of scalar multiplication we can combine the factors in the
desired vector pro duct to give:
3C · (2A × B) = 6C · (A × B) .
Evaluate A × B first:
A × B =
i j k
2.0 3.0 −4.0
−3.0 4.0 2.0
= (6.0 + 16.0)i + (12.0 − 4.0)j + (8.0 + 9.0)k
= 22.0i + 8.0j + 17.0k
Then:
C · (A × B) = (7.0)(22.0) − (8.0)(8.0) + (0.0)(17.0) = 90
So the answer we want is:
6C · (A ×B) = (6)(90.0) = 540
31. A student claims to have found a vector A such that
(2i − 3j + 4k) × A = (4i + 3j − k) .
Do you believe this c laim? E xplain. [Ser4 11-8]
Frankly, I’ve been in this teaching business so long and I’ve grown so c ynical that I don’t
believe anything any student claims anymore, and this case is no exception. But enough
about me; let’s see if we can provide a mathematic al answer.
We might try to work out a solution for A, but let’s think about some of the basic
properties of the cross product. We know that the cross product of two vectors must be
perpendicular to each of the “multiplied” vectors. So if the student is tell ing the truth, it
must be true that (4i + 3j − k ) i s perpendicular to (2i − 3j + 4k). Is it?
We can test this by taking the dot product of the two vectors:
(4i + 3j − k) · (2i − 3j + 4k) = (4)(2) + (3)(−3) + (−1)(4) = −5 .
The dot product does not give zero as it must if the two vectors are perpendicular. So we
have a contradic tion. There can’t be any vector A for which the relation is true.
